TOP: Trajectory Optimization via Parallel Optimization towards Constant Time Complexity

Abstract

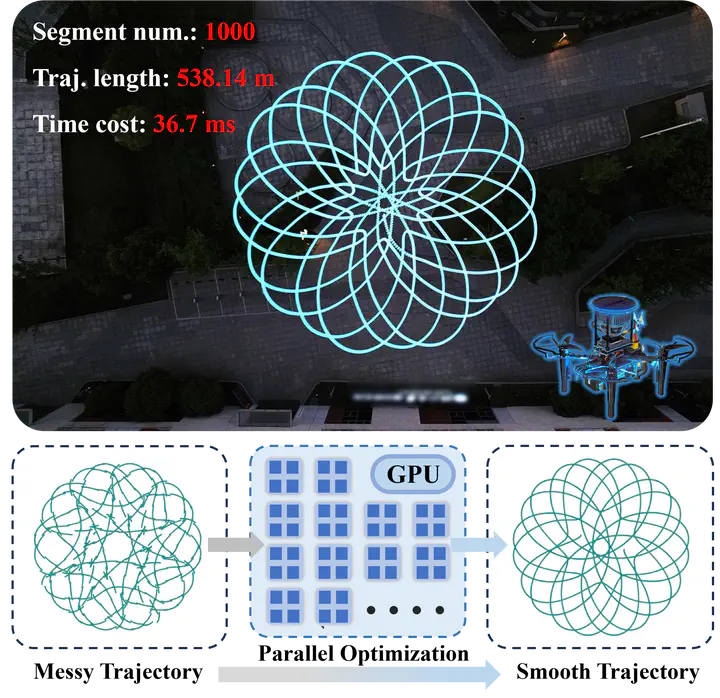
Optimization has been widely used to generate smooth trajectories for motion planning. However, existing trajectory optimization methods show weakness when dealing with large-scale long trajectories. Recent advances in parallel computing have accelerated optimization in some fields, but how to efficiently solve trajectory optimization via parallelism remains an open question. In this paper, we propose a novel trajectory optimization framework based on the Consensus Alternating Direction Method of Multipliers (CADMM) algorithm, which decomposes the trajectory into multiple segments and solves the subproblems in parallel. The proposed framework reduces the time complexity to (O(1)) per iteration with respect to the number of segments, compared to (O(N)) of the state-of-the-art (SOTA) approaches. Furthermore, we introduce a closed-form solution that integrates convex linear and quadratic constraints to speed up the optimization, and we also present a numerical solution for general convex inequality constraints. A series of simulations and experiments demonstrate that our approach outperforms the SOTA approach in terms of efficiency and smoothness. Especially for a large-scale trajectory, with one hundred segments, achieving over a tenfold speedup. To fully explore the potential of our algorithm on modern parallel computing architectures, we deploy our framework on a GPU and show high performance with thousands of segments.